Answer:
a) the expected flow rate is 31.4 ft³/s
b) the required brake horsepower is 2808.4 bhp
c) the location of pump inlet to avoid cavitation is -8.4 ft
Step-by-step explanation:
Given the data in the question;
free surface elevation = 200 ft
total length of pipe required = 1000 ft
diameter = 12 inch
Iron with relative roughness ( k/D ) = 0.0005
H
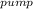 = 665-0.051Q² [Qinft ]
= 665-0.051Q² [Qinft ]
a) the expected flow rate
given that;
k/D = 0.0005
k/2R = 0.0005
R/k = 1000
now, we determine the friction factor;
1/√f = 2log₁₀( R/k ) + 1.74
we substitute
1/√f = 2log₁₀( 1000 ) + 1.74
1/√f = 6 + 1.74
1/√f = 7.74
√f = 1/7.74
√f = 0.1291989
f = (0.1291989)²
f = 0.01669
Now, Using Bernoulli theorem between two reservoirs;
(p/ρq)₁ + (v²/2g)₁ + z₁ + H
 = (p/ρq)₂ + (v²/2g)₂ + z₂ + h
= (p/ρq)₂ + (v²/2g)₂ + z₂ + h

so
0 + 0 + 0 + 665-0.051Q² = 0 + 0 + 200 + flQ²/2gdA²
665-0.051Q² = 200 + flQ²/2gdA²
665-0.051Q² = 200 +[ ( 0.01669 × 1000 × Q² ) / (2 × 32.2 × (π/4)² × 1⁵ )
665 - 0.051Q² = 200 + [ 16.69Q² / 39.725 ]
665 - 200 - 0.051Q² = 0.420138Q²
665 - 200 = 0.420138Q² + 0.051Q²
465 = 0.471138Q²
Q² = 465 / 0.471138
Q² = 986.97196
Q = √986.97196
Q = 31.4 ft³/s
Therefore, the expected flow rate is 31.4 ft³/s
b) the brake horsepower required to drive the pump (assume an efficiency of 78%).
we know that;
P = ρgH
 Q / η
Q / η
where; H
 = 665 - 0.051(986.97196) = 614.7
= 665 - 0.051(986.97196) = 614.7
we substitute;
P = ( 62.42 × 614.7 × 31.4 ) / ( 0.78 × 550 )
P = 1204804.6236 / 429
P = 2808.4 bhp
Therefore, the required brake horsepower is 2808.4 bhp
c) the location of pump inlet to avoid cavitation (assume the required NPSH=25 ft).
NPSH = (
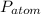 / ρg) - h
/ ρg) - h
 - ( P
- ( P
 / ρg )
/ ρg )
we substitute
25 = ( 2116 / 62.42 ) - h
 - ( 30 / 62.42 )
- ( 30 / 62.42 )
h
 = 8.4 ft
= 8.4 ft
Therefore, the location of pump inlet to avoid cavitation is -8.4 ft