Question

Multiple incorrect password attempts for a single login can, of course, sometimes be suggestive of an attempt to gain unauthorized access to an account. Typically there are about 52 such attempts noted each day. An analyst examining web server logs notes what appears to be an increase in these incidents over the previous 30 days in which there were an average of 57 attempts each day with a standard deviation of 17.2. Has there been a statistically significant increase in the number of attempts? Use the standard level for alpha.

Answer 1

The p-value of the test is 0.0613 > 0.05, which means that there has not been a statistically significant increase in the number of attempts.

Explanation:

Typically there are about 52 such attempts noted each day. Test if there has been a statistically significant increase.

At the null hypothesis, we test if the mean is the same, that is of 52. Thus:

`H_0: \mu = 52`

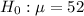
At the alternative hypothesis, we test if there has been an increase, that is, if the mean is greater than 52. So

`H_1: \mu > 52`

Use the standard level for alpha.

So
`\alpha = 0.05`

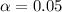
The test statistic is:

We have the standard deviation for the sample, so t-distribution.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

52 is tested at the null hypothesis:

This means that
`\mu = 52`

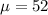
Over the previous 30 days in which there were an average of 57 attempts each day with a standard deviation of 17.2.

This means that
`n = 30, X = 57, s = 17.2`

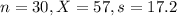
Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (57 - 52)/((17.2)/(√(30)))`

`t = 1.59`

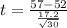
P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean above 57, which is a right-tailed test with t = 1.59 and 30 - 1 = 29 degrees of freedom.

Using a t-distribution calculator, this p-value is of 0.0613.

The p-value of the test is 0.0613 > 0.05, which means that there has not been a statistically significant increase in the number of attempts.