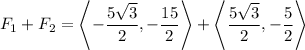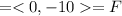Solution :
Let
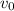 be the unit vector in the direction parallel to the plane and let
be the unit vector in the direction parallel to the plane and let
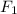 be the component of F in the direction of
be the component of F in the direction of
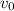 and
and
 be the component normal to
be the component normal to
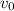 .
.
Since,
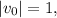
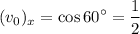
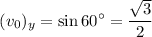
Therefore,
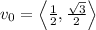
From figure,
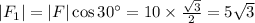
We know that the direction of
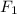 is opposite of the direction of
is opposite of the direction of
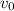 , so we have
, so we have

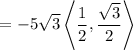
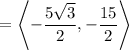
The unit vector in the direction normal to the plane,
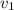 has components :
has components :
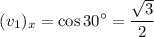
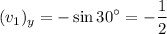
Therefore,
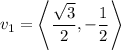
From figure,
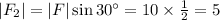
∴
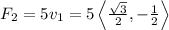
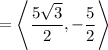
Therefore,