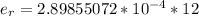Question

A square plate of titanium is 12cm along the top, 12cm on the right side, and 5mm thick. A normal tensile force of 15kN is applied to the top side of the plate. A normal tensile force of 20kN is applied to the right side of the plate. The elastic modulus, E, is 115 GPa for titanium.If the left and bottom edges of the plate are fixed, calculate the normal strain and elongation of both the TOP and RIGHT side of the plate.

Answer 1

`X_t=2.17391304*10^(-4)`

`X_r=2.89855072*10^(-4)`

`e_t=0.0026`

`e_r=0.0035`

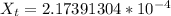
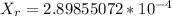
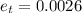
Step-by-step explanation:

From the question we are told that:

Dimension
`12*12`

Thickness
`l_t=5mm=5*10^-3`

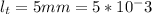
Normal tensile force on top side
`F_t= 15kN`

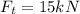
Normal tensile force on right side
`F_r= 20kN`

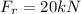
Elastic modulus,
`E=115Gpap=>115*10^9`

Generally the equation for Normal Strain X is mathematically given by

`X=(Force)/(Area*E)`

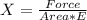
Therefore

For Top

`X_t=(Force_t)/(Area*E)`

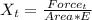
Where

`Area=L*B*T`

`Area=12*10^(-2)*5*10^(-3)`

`Area=6*10^(-4)`

`X_t=(15*10^3)/(6*10^(-4)*115*10^9)`

`X_t=2.17391304*10^(-4)`

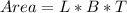
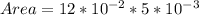
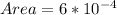
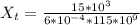
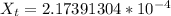
For Right side
`X_r=(Force_r)/(Area*E)`

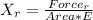
Where

Area=L*B*T

`Area=12*10^(-2)*5*10^(-3)`

`Area=6*10^(-4)`

`X_r=2.89855072*10^(-4)`

`X_r=2.89855072*10^(-4)`

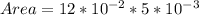
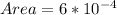
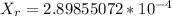
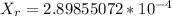
Generally the equation for elongation is mathematically given by

`e=strain *12`

For top

`e_t=2.17391304*10^(-4)*12`

`e_t=0.0026`

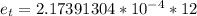
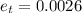
For Right

`e_r=2.89855072*10^(-4) *12`

`e_r=0.0035`