Question

Find the critical points of the given function and then determine whether they are local maxima, local minima, or saddle points.

f (x, y) = x^2 + y^2 + 2xyf(x,y)=x 2 +y 2 +2xy

Answer 1

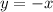`y =-x` ---- critical point

local minima

Explanation:

Given

`f(x,y) = x^2 + y^2 + 2xy`

Required

Determine the critical point

Differentiate w.r.t x

`f_x =2x + 2y`

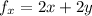
Differentiate w.r.t y

`f_y =2y + 2x`

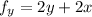
Equate both to 0

`2x + 2y =0`

`2y =0-2x`

`2y =-2x`

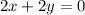
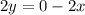
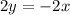
Divide by 2

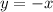`y =-x` ----- in both equations

Hence:

The critical point is:
`y =-x`

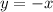
Solving (b):

We have:

`f_x =2x + 2y`

`f_y =2y + 2x`

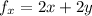
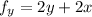
This is represented as:

`D = \left[\begin{array}{cc}2&2\\2&2\end{array}\right]`

Calculate the determinant

`|D| =2 * 2 -2 * 2`

`|D| = 4-4`

`|D| = 0`

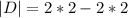
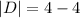
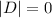
The critical point is at local minima