Question

Pseudomonas putida is used for fermentation of the lactose present in cheese whey. The bacteria are cultivated in a steady-state chemostat with sterile feed and at a dilution rate of D = 0.28 h-1. The lactose concentration in the feed and the effluent are S0 = 2.0 g/L and S = 0.10 g/L, respectively. The following information is available: YX/S = 0.45 g X/g S, YX/O2 = 0.25 g X/g O2, and C* = 8 mg/l (saturation DO). a. Determine the steady-state biomass concentration (X) and the specific rate of oxygen consumption (go2) b. What should be the oxygen transfer coefficient (Kia) to overcome oxygen transfer limitations if the desired DO concentration in the fermentation medium is 2 mg/l?

Answer 1

Step-by-step explanation:

Given that:

The dilution rate D = 0.28 h⁻¹

The concentration of lactose in the feed
`S_o = 2.0 \ g/L`

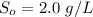
The effluent S = 0.10 g/L

Also;

`Y_(X/S) = 0.45 g\ X/g \ S , \\ \\ Y_(X/O2 )= 0.25 g \ X/g \ O2, \\ \\`

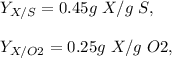
Saturation C* = 8 mg/l

To calculate the steady-state biomass, we use the formula:

`X = Y_(X/S)(S_o-S_e) \\ \\ X = 0.45(2.0 -0.10) \ g/L \\ \\ X= 0.45 (1.9) \ g/L \\ \\ X = 0.855\ g/L \\ \\ X = 855 \ mg/L`

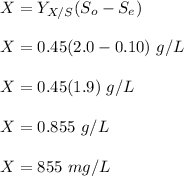
The biomass is 0.855 g/L

For a steady-state condition, the oxygen uptake rate can be illustrated by using the formula:

`q_(o_2)X =(\mu_X)/(Y_(X/O_2))`

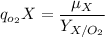
where;

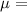`\mu =` dilution rate (D)

Thus, the steady-state can be expressed as:

`q_(o_2)X =(D)/(Y_(X/O_2))`

`q_(o_2)X =(0.28)/(0.25)`

`q_(o_2)X =1.12 \ h^(-1)`

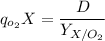
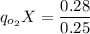
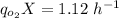
The specific rate of oxygen consumption
`q_(o_2)X =1.12 \ h^(-1)`

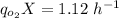
b)

In the fermentation medium, if the desired DO concentration
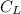`C_L` = 2 mg/L

Here, the oxygen transfer is regarded as the rate-limiting step.

As such, the oxygen transfer rate(OTR) is equivalent to the oxygen uptake rate.

In this scenario, let's determine the oxygen transfer coefficient
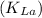`(K_(La))` by using the formula:

`OTR = K_(La)(C^* - C_L)`

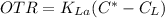
where;

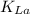`K_(La)`= coefficient of oxygen transfer

C* = saturation

Since
`OTR = q_(O_2)X`

`q_(o2)X = K_(La)(C^*-C_L) \\\\ (1.12 )(855) = K_(La)(8-2) \\ \\ 957.6 = K_La (6) \\ \\ K_(La)= (957.6)/(6) \\ \\ K_(La) = 159.6 \ h^(-1)`

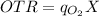
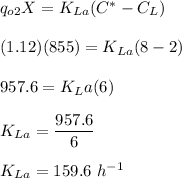
Thus, the oxygen transfer coefficient
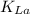`K_(La)` = 159.6 h⁻¹