Question

A container in the shape of this cuboid holds 2 litres of water.

The container has a square base.
Its height is double the length of each edge on its base.
Work out the height of the container, in cm.

Answer 1

Given:

Volume of cuboid container = 2 litres

The container has a square base.

Its height is double the length of each edge on its base.

To find:

The height of the container.

Solution:

We know that,

1 litre = 1000 cubic cm

2 litre = 2000 cubic cm

Let x be the length of each edge on its base. Then the height of the container is:

`h=2x`

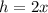
The volume of a cuboid is:

`V=l* w* h`

Where, l is length, w is width and h is height.

Putting
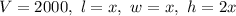`V=2000,\ l=x,\ w=x,\ h=2x`, we get

`2000=x* x* 2x`

`2000=2x^3`

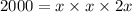
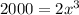
Divide both sides by 2.

`1000=x^3`

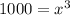
Taking cube root on both sides.

`\sqrt[3]{1000}=x`

`10=x`

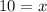
Now, the height of the container is:

`h=2x`

`h=2(10)`

`h=20`

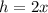
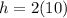
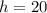
Therefore, the height of the container is 20 cm.