Question

If GJ = 11a and IJ = a + 10, find the value of a that makes quadrilateral FGHI a parallelogram​

Answer 1

Note: Consider J is the intersection point of diagonals of quadrilateral FGHI.

Given:

`GJ=11a`

`IJ=a+10`

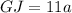
To find:

The value of a that makes quadrilateral FGHI a parallelogram​.

Solution:

We know that the diagonals of a parallelogram bisect each other.

If FGHI is a parallelogram​ and J is the intersection point of diagonals, then

`GJ=IJ`

`11a=a+10`

`11a-a=10`

`10a=10`

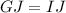
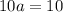
Divide both sides by 10.

`a=(10)/(10)`

`a=1`

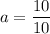
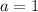
Therefore, the required value of a is 1 units.