Answer:
Options (1), (2), (3) and (7)
Explanation:
Given expression is
![\frac{\sqrt[3]{8^{(1)/(3)}* 3} }{3*2^{(1)/(9)}}](https://img.qammunity.org/2022/formulas/mathematics/college/ksiuflib1lwpvfqo4xd67mzsfyiifchpoc.png) .
.
Now we will solve this expression with the help of law of exponents.
![\frac{\sqrt[3]{8^{(1)/(3)}* 3} }{3*2^{(1)/(9)}}=\frac{\sqrt[3]{(2^3)^{(1)/(3)}* 3} }{3*2^{(1)/(9)}}](https://img.qammunity.org/2022/formulas/mathematics/college/zrubhfxal1f3c8dzu8bdfsfvopxem614n5.png)
![=\frac{\sqrt[3]{2* 3} }{3*2^{(1)/(9)}}](https://img.qammunity.org/2022/formulas/mathematics/college/wg5r6y7450if1ji51q1p47hm0beryc6ss5.png)
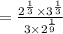

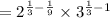
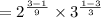
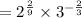 [Option 2]
[Option 2]
![2^{(2)/(9)}* 3^{-(2)/(3) }=(\sqrt[9]{2})^2* (\sqrt[3]{(1)/(3) } )^2](https://img.qammunity.org/2022/formulas/mathematics/college/ylv39pu4mu4w9btgpmye8371mv4v79wdm3.png) [Option 1]
[Option 1]
![2^{(2)/(9)}* 3^{-(2)/(3) }=(\sqrt[9]{2})^2* (\sqrt[3]{(1)/(3) } )^2](https://img.qammunity.org/2022/formulas/mathematics/college/ylv39pu4mu4w9btgpmye8371mv4v79wdm3.png)
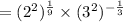
![=\sqrt[9]{4}* \sqrt[3]{(1)/(9) }](https://img.qammunity.org/2022/formulas/mathematics/college/fr1w71czh02euoorusse8a1gw8lhxyxc2p.png) [Option 3]
[Option 3]
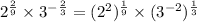
![=\sqrt[9]{2^2}* \sqrt[3]{3^(-2)}](https://img.qammunity.org/2022/formulas/mathematics/college/bo1q47jp4zi3fi25pfe1549wsjg4mf7ov8.png) [Option 7]
[Option 7]
Therefore, Options (1), (2), (3) and (7) are the correct options.