Question

Can you find the limits of this ​

Answer 1

`\displaystyle \lim_(x \to -2) (x^3 + 8)/(x^4 - 16) = (-3)/(8)`

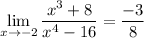
General Formulas and Concepts:

Calculus

Limits

Limit Rule [Constant]:
`\displaystyle \lim_(x \to c) b = b`

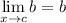
Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

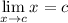
Limit Property [Addition/Subtraction]:
`\displaystyle \lim_(x \to c) [f(x) \pm g(x)] = \lim_(x \to c) f(x) \pm \lim_(x \to c) g(x)`

L'Hopital's Rule

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Explanation:

We are given the following limit:

`\displaystyle \lim_(x \to -2) (x^3 + 8)/(x^4 - 16)`

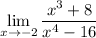
Let's substitute in x = -2 using the limit rule:

`\displaystyle \lim_(x \to -2) (x^3 + 8)/(x^4 - 16) = ((-2)^3 + 8)/((-2)^4 - 16)`

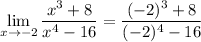
Evaluating this, we arrive at an indeterminate form:

`\displaystyle \lim_(x \to -2) (x^3 + 8)/(x^4 - 16) = (0)/(0)`

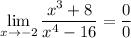
Since we have an indeterminate form, let's use L'Hopital's Rule. Differentiate both the numerator and denominator respectively:

`\displaystyle \lim_(x \to -2) (x^3 + 8)/(x^4 - 16) = \lim_(x \to -2) (3x^2)/(4x^3)`

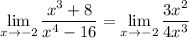
Substitute in x = -2 using the limit rule:

`\displaystyle \lim_(x \to -2) (3x^2)/(4x^3) = (3(-2)^2)/(4(-2)^3)`

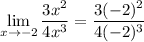
Evaluating this, we get:

`\displaystyle \lim_(x \to -2) (3x^2)/(4x^3) = (-3)/(8)`

And we have our answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits