Given:
The parent function is:
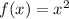
This function shift 1 unit left, vertically stretch by a factor of 3 and reflected over the x-axis.
To find:
The function after the given transformations.
Explanation:
The transformation is defined as
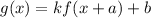 ... (i)
... (i)
Where, k is stretch factor, a is horizontal shift and b is vertical shift.
If k<0, then the graph of f(x) is reflected over the x-axis.
If 0<|k|<1, then the graph compressed vertically by factor |k| and if |k|>1, then the graph stretch vertically by factor |k|.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.
It is given that the graph of f(x) shifts 1 unit left, so a=1.
The graph of f(x) vertically stretch by a factor of 3, so |k|=3.
The graph of f(x) reflected over the x-axis, so k=-3.
There is no vertical shift, so b=0.
Putting
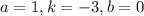 in (i), we get
in (i), we get
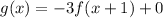
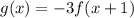
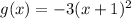
![[\because f(x)=x^2]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ypsimcjroqn66hkis8zs62mn92djr9sj4g.png)
Therefore, the correct option is B.