Explanation:
Given that,
The length of a ladder, H = 20 feet
The height of the wall, h = 15 ft
We know that,
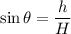
h is perpendicular and H is hypotenuse
So,
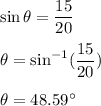
Now using Pythagoras theoerm,
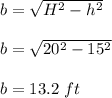
Hence, the angle made by the ladder and the ground is 48.59° and the ladder is 13.2 feet from the wall on the ground.