Question

What are all the real zeros of y=(x-20)^2 +5

Please show step by step I'm so lost

Answer 1

no real zeros

Explanation:

We are given the following quadratic function:

`y = {(x - 20)}^(2) + 5`

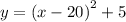
firstly simplify it to standard form which is

`y = {x}^(2) -40x + 405`

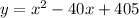
To figure out the real zeros, set y to 0:

`{x}^(2) - 40x + 405 = 0`

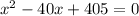
recall that,a quadratic equations has real zeros in case its discriminant is greater than or equal to 0, therefore

• b²-4ac≥0⇒real roots

consider,

• a=1
• b=-40
• c=405

now substitute:

`{ (- 40)}^(2) - 4(1)(405) \stackrel{ ? }{ \geq}0`

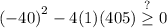
simplifying yields:

`1600 - 1620 \stackrel{ ? }{ \geq}0 \\ - 20 \\geq 0`

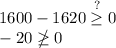
hence, The function has no real zeros

Answer 2

Simplify

`\\ \rm\longmapsto y=(x-20)^2+5`

`\\ \rm\longmapsto y=x^2-40x+405`

Graph attached

• No real zeros