Question

When a mass of 3.0-kg is hung on a vertical spring, it stretches by 0.085 m. Determine

the period of oscillation of a 4.0-kg object suspended from this spring.

Answer 1

the period of oscillation of the given object is 0.14 s

Step-by-step explanation:

Given;

mass of the object, m = 3 kg

extension of the spring, x = 0.085 m

The spring constant is calculated as follows;

`F = mg = (1)/(2) ke^2\\\\2mg = ke^2\\\\k = (2mg)/(e^2) \\\\k = (2* 3 * 9.8)/((0.085)^2) \\\\k = 8,138.41 \ N/m`

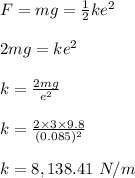
The angular speed of a 4 kg object is calculated as follows;

`\omega = \sqrt{(k)/(m) } \\\\(2\pi )/(T) = \sqrt{(k)/(m) } \\\\T= 2\pi \sqrt{(m)/(k) } \\\\T = 2\pi \sqrt{(4)/(8138.41) }\\\\T = 0.14 \ s`

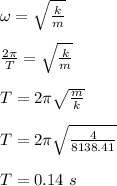
Therefore, the period of oscillation of the given object is 0.14 s