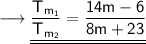Question

Question -

If the ratio of the sums of first n^th terms of two AP's is (7n + 1):(4n + 27) find the ratio of their m^th terms.​

Answer 1

`\rule{200}4`

Answer : The required ratio is (14m-6):(8m+23) .

`\rule{200}4`

Here we are given that the ratio of sum of first n terms of two AP's is (7n + 1):(4n + 27) .

That is.

`\small\sf\longrightarrow (S_1)/(S_2)=(7n +1)/(4n +27) \\`

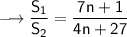
As , we know that the sum of n terms of an AP is given by ,

`\small\sf\longrightarrow \pink{ S_n =(n)/(2)[2a +(n-1)d]} \\`

Assume that ,

• First term of 1st AP = a
• First term of 2nd AP = a'
• Common difference of 1st AP = d
• Common difference of 2nd AP = d'

Using this we have ,

`\small\sf\longrightarrow (S_1)/(S_2)=((n)/(2)[2a + (n-1)d])/((n)/(2)[2a' +(n-1)d'] ) \\`

`\small\sf\longrightarrow (7n+1)/(4n+27)=(2a + (n -1)d)/(2a' + (n -1)d' ) . . . . . (i) \\`

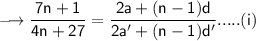
Now also we know that the nth term of an AP is given by ,

`\longrightarrow\sf\small \pink{ T_n = a + (n-1)d}\\`

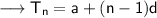
Therefore,

`\longrightarrow\sf\small (T_(m_1))/(T_(m_2))= ( a + (n-1)d )/(a'+(n-1)d'). . . . . (ii)\\`

`\longrightarrow\sf\small (T_1)/(T_2)=(2a + (2n-2)d)/(2a'+(2n-2)d') . . . . . (iii)\\`

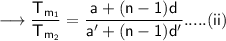
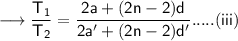
From equation (i) and (iii) ,

`\longrightarrow\sf\small n-1 = 2m-2\\`

`\longrightarrow\sf\small n = 2m -2+1 \\`

`\longrightarrow\sf\small n = 2m -1 \\`

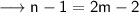
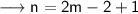
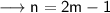
Substitute this value in equation (i) ,

`\longrightarrow \sf\small (2a+ (2m-1-1)d)/(2a' +(2m-1-1)d')=(7(2m-1)+1)/(4(2m-1) +27)\\`

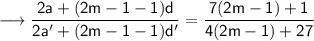
Simplify,

`\longrightarrow\sf\small ( 2a + (2m-2)d)/(2a' +(2m-2)d')=(14m-7+1)/(8m-4+27)\\`

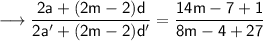
`\longrightarrow\sf\small (2[a + (m-1)d])/(2[a' + (m-1)d'])=( 14m-6)/(8m+23)\\`

`\longrightarrow\sf\small ([a + (m-1)d])/([a' + (m-1)d'])=( 14m-6)/(8m+23)\\`

From equation (ii) ,

`\longrightarrow\sf\small \underline{\underline{\blue{ (T_(m_1))/(T_(m_2))=( 14m-6)/(8m+23)}}}\\`

`\rule{200}4`