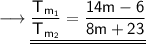Answer : The required ratio is (14m-6):(8m+23) .

Here we are given that the ratio of sum of first n terms of two AP's is (7n + 1):(4n + 27) .
That is.
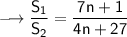
As , we know that the sum of n terms of an AP is given by ,
![\small\sf\longrightarrow \pink{ S_n =(n)/(2)[2a +(n-1)d]} \\](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/s2344p7klnthlqnej875.png)
Assume that ,
- First term of 1st AP = a
- First term of 2nd AP = a'
- Common difference of 1st AP = d
- Common difference of 2nd AP = d'
Using this we have ,
![\small\sf\longrightarrow (S_1)/(S_2)=((n)/(2)[2a + (n-1)d])/((n)/(2)[2a' +(n-1)d'] ) \\](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/12ihxhpc4h3t6xeib8jm.png)

Now also we know that the nth term of an AP is given by ,
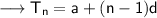
Therefore,
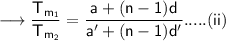
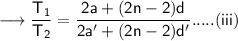
From equation (i) and (iii) ,
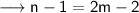
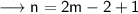
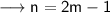
Substitute this value in equation (i) ,
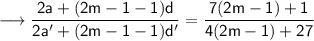
Simplify,
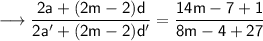
![\longrightarrow\sf\small (2[a + (m-1)d])/(2[a' + (m-1)d'])=( 14m-6)/(8m+23)\\](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/x0skh641ry9v2a7v6s2q.png)
![\longrightarrow\sf\small ([a + (m-1)d])/([a' + (m-1)d'])=( 14m-6)/(8m+23)\\](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/3iqbegyw25dmjci01x50.png)
From equation (ii) ,