Answer:
The radius of Circle D is 8 cm.
The perimeter of ΔABC is (24 + 6√7) cm.
Explanation:
First, let the intersection point below D be K and let the intersection point between A and B be J.
Since segment BK, which passes through the center of the circle, is perpendicular to chord AC, BK also bisects AC. Hence, AK = CK.
Connect points A and D to create radius AD. Note that BD is also a radius. Hence, AD = BD.
For ΔABK, by the Pythagorean Theorem:
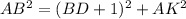
Since AB = 12:

For ΔADK, by the Pythagorean Theorem:

Since AD = BD:
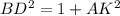
Subtract the second equation into the first:
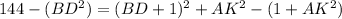
Simplify:
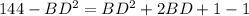
Hence:
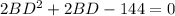
Simplify:
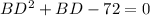
Factor:
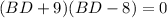
By the Zero Product Property:

Since the radius must be positive, the radius is 8 cm.
Since we already know AB and BC, we need to find AC to find the perimeter.
Note that AC = AK + CK = 2AK.
From the second equation:
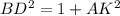
Thus:

Hence:
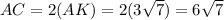
Therefore, the perimeter of ΔABC is:
