Answer:
T = 56.11 N
Step-by-step explanation:
Given that,
The equation of a wave is :
y = 0.08 sin(469t – 28.0x),
where x and y are in meters and t is in seconds
The linear mass density of the wave = 0.2 kg/m
The speed of wave is given by :
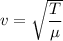
Also,
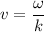
We have,
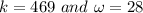
Put all the values,
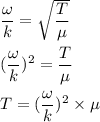
Put all the values,
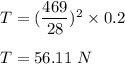
So, the tension in the string is 56.11 N.