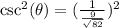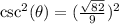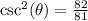Question

Given tan theta =9, use trigonometric identities to find the exact value of each of the following:_______

a) sec sqr Theta
b) Cot theta
c) cot (pie/2-Theta)
d) csc sqr theta

Answer 1

`(a)\ \sec^2(\theta) = 82`

`(b)\ \cot(\theta) = (1)/(9)`

`(c)\ \cot((\pi)/(2) - \theta) = 9`

`(d)\ \csc^2(\theta) = (82)/(81)`

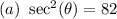
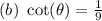
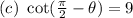
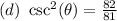
Explanation:

Given

`\tan(\theta) = 9`

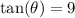
Required

Solve (a) to (d)

Using tan formula, we have:

`\tan(\theta) = (Opposite)/(Adjacent)`

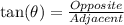
This gives:

`(Opposite)/(Adjacent) = 9`

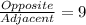
Rewrite as:

`(Opposite)/(Adjacent) = (9)/(1)`

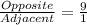
Using a unit ratio;

`Opposite = 9; Adjacent = 1`

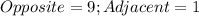
Using Pythagoras theorem, we have:

`Hypotenuse^2 = Opposite^2 + Adjacent^2`

`Hypotenuse^2 = 9^2 + 1^2`

`Hypotenuse^2 = 81 + 1`

`Hypotenuse^2 = 82`

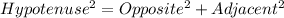
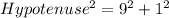
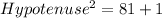
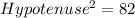
Take square roots of both sides

`Hypotenuse =√(82)`

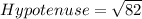
So, we have:

`Opposite = 9; Adjacent = 1`

`Hypotenuse =√(82)`

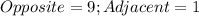
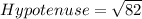
Solving (a):

`\sec^2(\theta)`

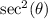
This is calculated as:

`\sec^2(\theta) = (\sec(\theta))^2`

`\sec^2(\theta) = ((1)/(\cos(\theta)))^2`

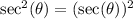
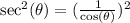
Where:

`\cos(\theta) = (Adjacent)/(Hypotenuse)`

`\cos(\theta) = (1)/(√(82))`

So:

`\sec^2(\theta) = ((1)/(\cos(\theta)))^2`

`\sec^2(\theta) = ((1)/((1)/(√(82))))^2`

`\sec^2(\theta) = (√(82))^2`

`\sec^2(\theta) = 82`

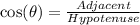
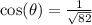
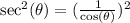
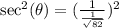
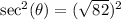
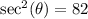
Solving (b):

`\cot(\theta)`

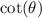
This is calculated as:

`\cot(\theta) = (1)/(\tan(\theta))`

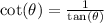
Where:

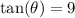`\tan(\theta) = 9` ---- given

So:

`\cot(\theta) = (1)/(\tan(\theta))`

`\cot(\theta) = (1)/(9)`

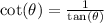
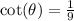
Solving (c):

`\cot((\pi)/(2) - \theta)`

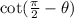
In trigonometry:

`\cot((\pi)/(2) - \theta) = \tan(\theta)`

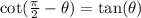
Hence:

`\cot((\pi)/(2) - \theta) = 9`

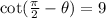
Solving (d):

`\csc^2(\theta)`

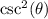
This is calculated as:

`\csc^2(\theta) = (\csc(\theta))^2`

`\csc^2(\theta) = ((1)/(\sin(\theta)))^2`

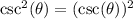
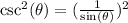
Where:

`\sin(\theta) = (Opposite)/(Hypotenuse)`

`\sin(\theta) = (9)/(√(82))`

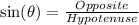
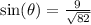
So:

`\csc^2(\theta) = ((1)/((9)/(√(82))))^2`

`\csc^2(\theta) = ((√(82))/(9))^2`

`\csc^2(\theta) = (82)/(81)`