Answer:
City A and city B will have equal population 25years after 1990
Explanation:
Given
Let
 years after 1990
years after 1990
 population function of city A
population function of city A
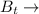 population function of city B
population function of city B
City A
 ---- initial population (1990)
---- initial population (1990)
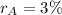 --- rate
--- rate
City B
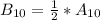 ----- t = 10 in 2000
----- t = 10 in 2000
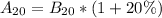 ---- t = 20 in 2010
---- t = 20 in 2010
Required
When they will have the same population
Both functions follow exponential function.
So, we have:
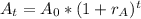
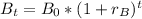
Calculate the population of city A in 2000 (t = 10)
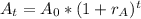

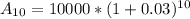

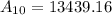
Calculate the population of city A in 2010 (t = 20)
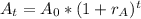
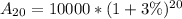
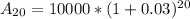
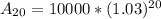
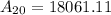
From the question, we have:
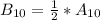 and
and
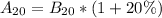
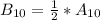


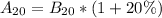

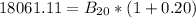
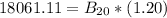
Solve for B20
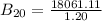

 and
and
 can be used to determine the function of city B
can be used to determine the function of city B
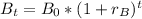
For:

We have:
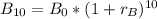

For:

We have:
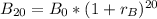

Divide
 by
by

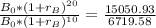
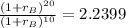
Apply law of indices
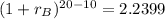
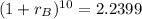 --- (1)
--- (1)
Take 10th root of both sides
![1 + r_B = \sqrt[10]{2.2399}](https://img.qammunity.org/2022/formulas/mathematics/college/op1bnvoyp61ff1eutndkwbcdhc8mf42kt8.png)
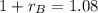
Subtract 1 from both sides
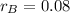
To calculate
 , we have:
, we have:

Recall that:
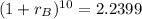
So:
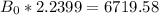
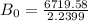
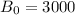
Hence:
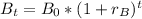
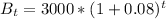
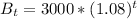
The question requires that we solve for t when:
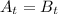
Where:
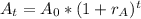
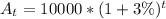
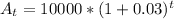
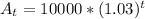
and
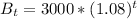
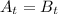 becomes
becomes

Divide both sides by 10000
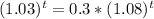
Divide both sides by
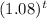
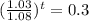
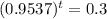
Take natural logarithm of both sides
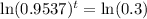
Rewrite as:

Solve for t


Approximate
