Question

A poll is given, showing 60% are in favor of a new building project.

If 7 people are chosen at random, what is the probability that exactly 5 of them favor the new building project?

Answer 1

Answer: 0.2612736

Round this value however you need to.

==================================================

Step-by-step explanation:

• n = 7 = sample size
• p = 0.60 = probability of someone being in favor
• k = 5 = number of people in favor

We use the binomial distribution here. The formula for that is

P(k) = (n C k)*(p)^k*(1-p)^(n-k)

where the n C k refers to the nCr combination formula

`_n C _r = (n!)/(r!*(n-r)!)`

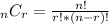
simply replace r with k.

------------------------------

So,

P(k) = (n C k)*(p)^k*(1-p)^(n-k)

P(5) = (7 C 5)*(0.6)^5*(1-0.6)^(7-5)

P(5) = 21*(0.6)^5*(0.4)^(2)

P(5) = 21*0.07776*0.16

P(5) = 0.2612736

This decimal value is exact (meaning there aren't any other digits after that last '6'). Round this value however you need to.

There's roughly a 26.1% chance of getting exactly 5 people to be in favor of the project.