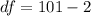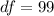Suppose you wanted to find a critical test statistic for a confidence interval for the slope of the regression line. How many degrees of freedom would you need to use?

Question

asked Sep 16, 2022 162k views

1 Answer

Karl Anka · Answer 1 · 2022-09-19T23:15:02+0000

Answer:

See Explanation

Explanation:

The question is incomplete, as the regression line is not given.

However, I will give a general explanation of how to calculate the degree of freedom of a slope of regression line

The degree of freedom is calculated using:

df = n - k

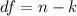
Where

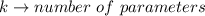
$k \to number\ of\ parameters$

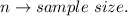
$n \to sample\ size.$

For a regression line; there are two parameters that are being estimates;

The intercept and the slope. So:

k = 2

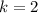
Hence, the degree of freedom of a slope of regression line is:

df = n -2

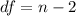
So; if for example

n =101

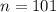
the degree of freedom will be:

df =101 - 2

df =99