Question

What is the constant of proportionality in the equation StartFraction x over y EndFraction StartFraction 2 over 9 EndFraction?

StartFraction 2 over 9 EndFraction
2
StartFraction 9 over 2 EndFraction
9

Answer 1

Given:

The equation is:

`(x)/(y)=(2)/(9)`

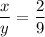
To find:

The constant of proportionality.

Solution:

If y is directly proportional to x, then

`y\propto x`

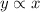
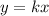`y=kx` ...(i)

Where, k is the constant of proportionality.

We have,

`(x)/(y)=(2)/(9)`

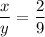
On cross multiplication, we get

`9x=2y`

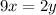
Divide both sides by 2.

`(9)/(2)x=y`

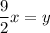
Interchange the sides.

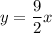`y=(9)/(2)x` ...(ii)

On comparing (i) and (ii), we get

`k=(9)/(2)`

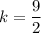
The constant of proportionality is
`(9)/(2)`. Therefore, the correct option is B.