Given:
Sum of all the interior angles of a regular polygon is 1080°.
Measure of each side is 10 cm.
To find:
The perimeter.
Solution:
The sum of all interior angles of a regular polygon with n side is:

Sum of all the interior angles of a regular polygon is 1080°.
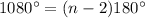
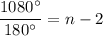
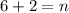
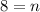
Number of sides of the regular polygon is 8. The measure of each side is 10 cm. So, the perimeter of the regular polygon is:
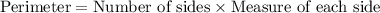
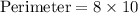
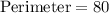
Therefore, the perimeter of the regular polygon is 80.