Answer:
Explanation:
I'll show you how to do the first one; the other are exactly the same, so pay attention.
The formula for arc length is
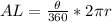 where θ is the central angle's measure. It just so happens that the measure of the central angle is the same as the measure of the arc it intercepts. Our arc shows a measure of 40°; this measure is NOT the same as the length. Measures are in degrees while length is in inches, or cm, or meters, etc. Going off that info, our central angle measures 40°. Filling in the formula and using 3.1415 for π:
where θ is the central angle's measure. It just so happens that the measure of the central angle is the same as the measure of the arc it intercepts. Our arc shows a measure of 40°; this measure is NOT the same as the length. Measures are in degrees while length is in inches, or cm, or meters, etc. Going off that info, our central angle measures 40°. Filling in the formula and using 3.1415 for π:
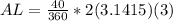 . I'm going to reduce that fraction a bit (and I'll use the same reduction in the Area of a sector coming up next):
. I'm going to reduce that fraction a bit (and I'll use the same reduction in the Area of a sector coming up next):
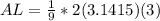 which makes
which makes
AL = 2.09 units. Now for Area of the Sector. The formula is almost identical, but instead uses the idea that the area of a circle is πr²:
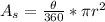 where θ is, again, the measure of the central angle (which is the same as the measure of the arc it intercepts). Filling in:
where θ is, again, the measure of the central angle (which is the same as the measure of the arc it intercepts). Filling in:
 which simplifies a bit to
which simplifies a bit to
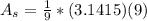 . As you can see, the 9's cancel each other out, leaving you with
. As you can see, the 9's cancel each other out, leaving you with
 units²
units²