Question

You toss six coins at the same time. how many possible outcomes are there?

64

36

12

6​

Answer 1

64 outcomes

Explanation:

• Let the number of coins be n.
• Let the number of outcomes per coin be X.

Given the following data;

Number of coins = 6

Number of outcomes for a single coin = 2

A single coin comprises of a head (H) and a tail (T), thus, the number of outcomes for a single coin is two (2).

To find how many possible outcomes we would have from tossing six coins at the same time, we would use the following formula;

`Number \; of \; outcomes = X^(n)`

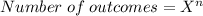
Substituting the values, we have;

Number of outcomes = 2⁶

2⁶ = 2 * 2 * 2 * 2 * 2 * 2

2⁶ = 64

Number of outcomes = 64

Therefore, the number of outcomes for a single coin tossed at the same time is equal to sixty four (64). It would have a total of 32 heads (H) and a total of 32 tails (T).