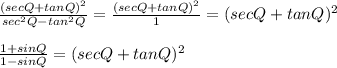Question

1-SinQ = (sec Q tanQ)2
1+sinQ​

Answer 1

The answer is below

Step-by-step explanation:

Prove that:

`(1+sinQ)/(1-sinQ)=(secQ + tanQ)^2`

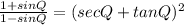
Trigonometric identities are equalities involving trigonometric functions for which both sides of the equality are equal and defined. Some trigonometric identities are:

sin²Ф + cos²Ф = 1; 1/cosФ = secФ; 1/sinФ = cosecФ; cosФ/sinФ = cotФ; 1 + tan²Ф = sec²Ф

Given:

`(1+sinQ)/(1-sinQ)\\\\Divide\ through\ by \ cosQ:\\\\ ((1)/(cosQ) +(sinQ)/(cosQ) )/((1)/(cosQ) -(sinQ)/(cosQ) )=(secQ+tanQ)/(secQ-tanQ)\\\\Next, rationalize\ the\ denominator\ by \ multiplying\ the\ numerator \ and\ \\denominator\ by\ secQ+tanQ:\\\\(secQ+tanQ)/(secQ-tanQ)*(secQ+tanQ)/(secQ+tanQ)=((secQ+tanQ)^2)/(sec^2Q+secQtanQ-secQtanQ-tan^2Q)\\\\=((secQ+tanQ)^2)/(sec^2Q-tan^2Q) ;\ But sec^2Q-tan^2Q=1,hence:\\\\`

`((secQ+tanQ)^2)/(sec^2Q-tan^2Q) =((secQ+tanQ)^2)/(1)=(secQ+tanQ)^2\\\\(1+sinQ)/(1-sinQ)=(secQ+tanQ)^2`