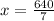Answer:
The car uses less gas
They use the same amount of gas after
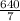 miles
miles
Explanation:
Given
The table represents the car mileage
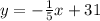 --- The van
--- The van
First, calculate the car's slope (m)

From the table, we have:
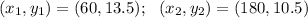
So, we have:
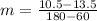
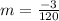
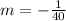
Calculate the equation using:


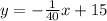
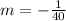 implies that for every mile traveled, the car uses 1/40 gallon of gas
implies that for every mile traveled, the car uses 1/40 gallon of gas
Also:
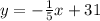 --- The van
--- The van
By comparison to:

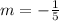
This implies that for every mile traveled, the van uses 1/5 gallon of gas.
By comparison:
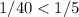
This means that the car uses less gas
Solving (b): Distance traveled for them to use the same amount of gas.
We have:
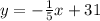 --- The van
--- The van
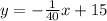 --- The car
--- The car
Equate both
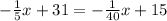
Collect like terms
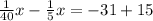

Take LCM
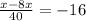

Solve for -7x
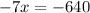
Solve for x