Answer:
i. The height of its jump is approximately 0.115 m
ii. The time of flight of its jump is approximately 0.306 seconds
iii. The range of its jump is approximately 0.795 m
Step-by-step explanation:
The angle at which the grasshopper jumps, θ = 30°
The speed with which the grasshopper takes off, u = 3 m/s
i. The height of its jump 'h', is given by the following relation;
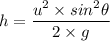
Where;
g = The acceleration due to gravity ≈ 9.81 m/s²
Therefore;
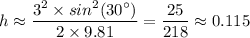
The height of its jump, h ≈ 0.115 m
ii. The time of flight of its jump, 't', is given as follows;
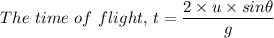
Therefore;
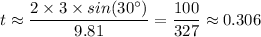
The time of flight of its jump, t ≈ 0.306 seconds
iii. The range of the jump is given by the following projectile motion equation for the range as follows;
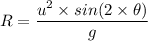
Therefore;

The range of the jump, R ≈ 0.795 m.