Question

Find the slope of the line that passes through (10, 4) and (6, 3).

Simplify your answer and write it as a proper fraction, improper fraction, or integer.

Answer 1

The slope of the line that pass through the points (10, 4), and (6, 3) is 1/4

Explanation:

The given points son the line are; (10, 4), and (6, 3)

The slope of a line is the rate of change of the y-values of the line relative to the x-values of the given line and the slope. 'm', can therefore be found by specifying two points on the line, (x₁, y₁), and (x₂, y₂), from which we get;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

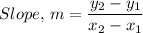
Therefore, the slope of the found line is given as follows;

(x₁, y₁) = (10, 4) and (x₂, y₂) = (6, 3)

`Slope \ of \ the \ line, \, m =(3-4)/(6-10) = (-1)/(-4) = (1)/(4)`

The slope of the line that pass through the points (10, 4), and (6, 3), m = 1/4