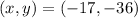Answer:
See explanation for matching pairs
Explanation:
Equations
(1)


(2)
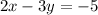
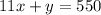
(3)
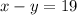
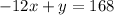
Solutions


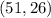
Required
Match equations with solutions
(1)
 and
and

Make x the subject in:

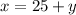
Substitute
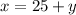 in
in

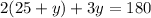
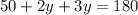
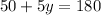
Collect like terms

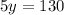
Solve for y
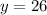
Recall that:
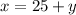
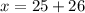
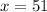
So:
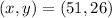
(2)
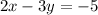 and
and
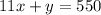
Make y the subject in
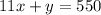

Substitute
 in
in
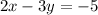

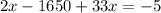
Collect like terms
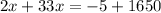
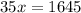
Solve for x
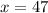
Solve for y in


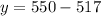
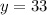
So:
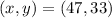
(3)
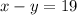 and
and
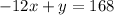
Make y the subject in
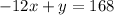
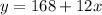
Substitute
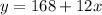 in
in
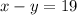
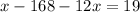
Collect like terms
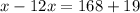
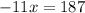
Solve for x
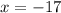
Solve for y in
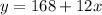

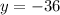
So: