Question

Find the domain and range. Show solution.


`y = (2)/(2x)`
Domain:
Range:​

Answer 1

We are given with a function y =2/(2x) . So , if we cancel the 2 from both numerator and denominator we are left with y = 1/x . Now , here we need to find the domain , bur let's Recall that Domain is the set of all values for which the given function is defined .Now , here , if we put x = 0 , then y will be not defined , but as for domain we need only the set of values for which the function is defined , so domain willn't include 0 , and for all real numbers except 0 , the given function is defined . So Our domain is
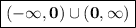`{\boxed{\bf{(-\infty,0)\cup (0,\infty)}}}` and as this interval contains all real numbers except 0 , so domain can be further written as
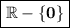`{\boxed{\mathbb{R}-\bf \{0\}}}` . Now , Range is the set of all output values of the function when we put the values of domain as input . So , now here when we put values of domain as input like let's put x = -1 , -2 , -3 , -4 , 1 , 2 , 3 ,..... we will get y = -1 , -1/2 , -1/3 , -1/4 , 1 , 1/2 , 1/3 and so on , now , the input will give output as 0 , iff input is Infinite , but as input can never be infinite, so output will never comes to 0 as the intervals of real numbers is
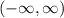`{\bf{(-\infty,\infty)}}` it's an open interval so Infinity and -ve infinity is not concluded in the above interval because whenever we think a number as large as much we can think , their exists infinitely large numbers greater than it , assume you're thinking 10¹⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰ as the largest number you can think , but if we add 1 in that i.e 10¹⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰ + 1 comes to be greater than it , Hence , we don't include Infinity and -ve Infinity in the interval which represents the set of all real numbers. So now the range is same as the Domain i.e
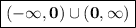`{\boxed{\bf{(-\infty,0)\cup (0,\infty)}}}` or
`{\boxed{\mathbb{R}-\bf \{0\}}}`

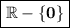
Hence , we concluded that :

• 
  `{\bf Domain=\mathbb{R}-\bf \{0\}}`
• 
  `{\bf Range=\mathbb{R}-\bf \{0\}}`
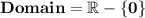
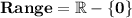
• Range = Domain