Question

You have reacted 100.00mL of 1.353M aqueous sulfuric acid with 12.618g of sodium hydroxide solid. If all of the heat generated by this reaction is transferred to a 1.317kg block of copper metal initially at 16.82°C, what is the final temperature of the block of copper metal? (Specific heat of copper = 0.375J/g*°C)

Answer 1

70.137 °C

Step-by-step explanation:

The reaction generated from the question can be expressed as:

`2NaOH_((s)) + H_2SO_(4(aq)) \to Na_2SO_(4(aq)) +2H_2O_((l))`

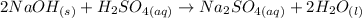
The enthalpy reaction:

`\Delta H^0 _(rxn) = \sum \Delta H^0 _(f (products)) - \sum \Delta H^0 _(f (reactants))`

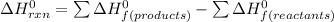
`\Delta H^0 _(rxn) =[2 * \Delta H^0 _f (H_2O) + \Delta H^0 _f (Na_2SO_4) ] -[2 \Delta * H^0 _f (NaOH) + \Delta H^0 _f (H_2SO_4) ]`

Repacing the values of each compound at standard enthalpy conditions;

`\Delta H^0 _(rxn) =[2 * -279.4 + (-1384.49)]-[(2* -418) -913]\ kJ`

`\Delta H^0 _(rxn) =-194.29 \ kJ`

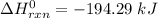
no of moles of NaOH = 12.618g/39.99 g/mol

= 0.3155 mol

no of moles of H₂SO₄ = molarity of H₂SO₄ × Volume

= 1.3553 mol/L × 100 × 10⁻³ L

= 0.13553 mol

From the reaction,

1 mol of NaOH = 2 × mol of H₂SO₄

Since mol of NaOH is greater than that of H₂SO₄, then NaOH is the excess reagent and H₂SO₄ is the limiting reactant

∴

1 mol of H₂SO₄ yields = - 194.29 kJ

0.13553 mol of H₂SO₄ will yield;

`= (-194.29 \ kJ)/(1 \ mol) * 0.13553 \ mol`

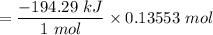
= -26.332124 kJ

= -26332.12 J

Finally,

Heat(q) =
`m_((copper)) * C_((copper))* \Delta T`

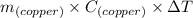
26332.12 J = 1.317 × 10³ g × 0.375 J/g°C ×ΔT

26332.12 J = 493.875 J/° C × ΔT

26332.12 / 493.875 = ΔT

ΔT = 53.317 °C

`T_f - T_i = 53.317 ^0 C`

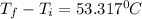
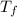`T_f`- 16.82 °C = 53.317 °C

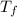`T_f` = (53.317 + 16.82) °C

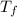`T_f` = 70.137 °C