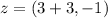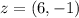Answer:
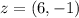
Explanation:
The missing parameters are:
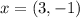
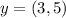
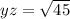 --- Hypotenuse
--- Hypotenuse
Required
The coordinate of Z
First, calculate the distance xy
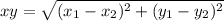
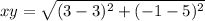
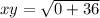
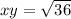
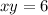
By Pythagoras theorem, distance xz is:
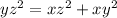
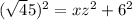
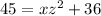
Collect like terms
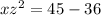
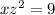
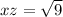
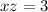
This means that z is 3 units to the right of x
We have:
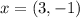
The rule to determine z is:
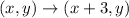
So, we have: