Question

The cost of a High Definition television now averages $700, but the cost is decreasing about 15% per year. In how many years will the cost be under $200?

Answer 1

Answer: 7.7 years

Explanation:

Given

The cost of HD TV is $700 and it is decreasing at the rate of 15% per year

After one year it becomes

`\Rightarrow 700-700* 15\%\\\Rightarrow 700(1-0.15)`

after 2 year it becomes

`\Rightarrow 700(1-0.15)-700(1-0.15)* 15\%\\\Rightarrow 700(1-0.15)(1-0.15)\\\Rightarrow 700(1-0.15)^2`

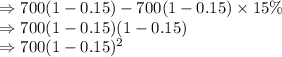
Suppose, after x years it becomes $200

`\Rightarrow 200=700(1-0.15)^x\\\\\Rightarrow (2)/(7)=0.85^x\\\\\text{Taking log both sides}\\\\\Rightarrow x=(\ln ((2)/(7)))/(\ln (0.85))\\\\\Rightarrow x=7.7\ \text{years}`

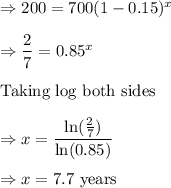
Thus, it takes 7.7 years for the cost to come under $200.