Question

A quadratic function has x-intercepts 2 and 6 and its vertex is (4, 8). What is the corresponding quadratic expression? A. 2x2 − 16x + 24 B. -2x2 + 16x – 24 C. -2x2 - 16x + 24 D. -x2 − 16x + 12 E. -x2 − 16x – 24

Answer 1

Given:

A quadratic function has x-intercepts 2 and 6 and its vertex is (4, 8).

To find:

The corresponding quadratic expression.

Solution:

If graph of a function intersect the x-axis at c, then (x-c) is a factor of the function.

A quadratic function has x-intercepts 2 and 6. It means (x-2) and (x-6) are two factors of the required quadratic function.

The function is defined as:

`P(x)=a(x-2)(x-6)` ...(i)

Where, a is a constant.

The vertex of the quadratic function is (4,8). It means the point (4,8) will satisfy the function.

Substituting x=4 and P(x)=8 in (i).

`8=a(4-2)(4-6)`

`8=a(2)(-2)`

`8=-4a`

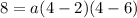
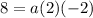
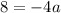
Divide both sides by -4.

`(8)/(-4)=a`

`-2=a`

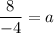
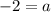
Putting
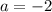`a=-2` in (i), we get

`P(x)=-2(x-2)(x-6)`

`P(x)=-2(x^2-6x-2x+12)`

`P(x)=-2(x^2-8x+12)`

`P(x)=-2x^2+16x-24`

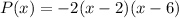
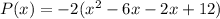
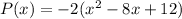
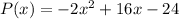
Therefore, the correct option is B.