Question

Ben asked his 19 classmates whether they were right handed or left-handed. There were five more right handed classmates than left handed classmates. Write a system of equations that can be used to determine how many of Ben’s classmates were right and left handed.

Answer 1

Answers:

The system of equations is

`\begin{cases}y = x-5\\x+y = 19\end{cases}`

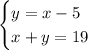
where x and y is the number of right-handed and left-handed people respectively.

The system solves to (x,y) = (12,7)

Interpretation:

There are 12 right-handed people and 7 left-handed people in the class.

=========================================================

Step-by-step explanation:

x = number of right-handed people

y = number of left-handed people

x and y are positive whole numbers.

There are 5 more right-handed people compared to left-handed people, so we can say x = y+5 which is the same as y = x-5. So you could go for either equation. Let's go for the one where y is isolated.

The second equation to form is x+y = 19 because there are 19 people in the class, and you can only be one or the other (left-handed or right-handed but not both). I'm not considering the possibility anyone is ambidextrous though of course that may happen in a realistic setting.

The two equations then form the system

`\begin{cases}y = x-5\\x+y = 19\end{cases}`

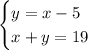
There are a number of ways we can solve this system. Substitution is possibly the quickest way.

x+y = 19

x+(x-5) = 19 ... replace y with x-5; due to the first equation

2x-5 = 19

2x = 19+5

2x = 24

x = 24/2

x = 12 .... this is the number of right-handed people

y = x-5

y = 12-5

y = 7 .... this is the number of left-handed people

Answer 2

left handed = 7 ; right handed = 12

Step-by-step explanation:

r = right handed

l = left handed

r + l = 19

r = l + 5

If we use substitution method we have:

l +5 + l = 19

2 l = 14

l = 7

r = 7 + 5 = 12