Question

City A is due north of City B. Find the distance between City A ​( north​ latitude) and City B ​( north​ latitude). Assume that the radius of Earth is 3960 miles.

The distance between City A and City B is ___miles.


Can someone help?! Show me step by step how this is done that I can understand it better.

Answer 1

Answer: 1679

=========================================================

Step-by-step explanation:

The notation
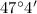`47^(\circ)4'` means "47 degrees, 4 minutes". The "minutes" isn't referring to a time value, but instead they are arc minutes. If we divide one degree into 60 equal pieces, then we form 60 arc minute slices. So in a sense, we are using a round analogue clock to help connect the two ideas.

We can convert to purely degrees through using this formula here

`a^(\circ)b' = a + (b)/(60)`

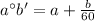
So,

`47^(\circ)4' = 47 + (4)/(60) \approx 47.06667^(\circ)`

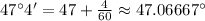
and similarly,

`22^(\circ)46' = 22+ (46)/(60) \approx 22.76667^(\circ)`

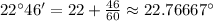
Now subtract the two results we got

47.06667-22.76667 = 24.3

The angular distance between the two cities is 24.3 degrees. By "angular distance" I basically mean how far you need to rotate your viewing angle when looking from city A to city B. Imagine that you're able to be situated at the center of the earth.

The circumference of the earth is

C = 2*pi*r

C = 2*pi*3960

C = 24,881.4138164311

which is approximate and the units are in miles. We multiply by the fraction 24.3/360 to find the arc distance along the curve that corresponds to the angle 24.3 degrees. This is because we don't want the whole circumference, but just a small fraction of it.

So (24.3/360)*24,881.4138164311 = 1,679.4954326091

This rounds to 1679

The distance between the two cities is about 1679 miles.

Answer 2

9514 1404 393

Answer:

1679 miles

Step-by-step explanation:

One minute is 1/60 of a degree, so the difference in latitudes is ...

47 4/60 -22 46/60 = 24 18/60 = 24.3 . . . degrees

The arc length is given by ...

s = rθ . . . . . . r = radius, θ = angle in radians

180° is π radians, so the surface distance between the two cities is ...

s = (3960 mi)(24.3×π/180) = 534.6π mi ≈ 1679.495 mi

The distance between City A and City B is about 1679 miles.

_____

Additional comment

As a good approximation, the distance is about 60 nautical miles per degree of latitude. Using that approximation, and converting from nautical miles to statute miles would give a distance of 1678 miles.