Question

Find the equation of straight line passing through the mid-point of (1,2) and (3,4) and having slope 3.

Note: write full steps​

Answer 1

`\large{ \tt{❃ \: EXPLANATION}} :`

• Let us assume the two points ( 1 , 2 ) and ( 3 , 4 ) be ( x₁ , y₁ ) and ( x₂ , y₂ ) respectively. Now , Find out the midpoint of those points :

`\boxed{\large{ \tt{✧ \: MIDPOINT = ( (x_(1) + x_(2))/(2) } \:, (y_(1) + y_(2))/(2) ) }}`

`\large{ \tt{↦ \: ( (1 + 3)/(2) \: , (2 + 4)/(2) )}}`

`\large{ \tt{↦( (4)/(2) \:, (6)/(2) })}`

`\large{ \tt{↦ \underline{( \: 2 \:, 3 \: )}}}`

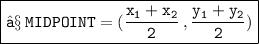
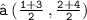
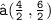
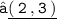
• To find the equation of straight line passing through a point and a slope , we use the equation of straight line in point slope form i.e y - y₁ = m ( x - x₁ ).

• We have : Slope ( m ) = 3 & assume the midpoint of ( 1 , 2 ) and ( 3 , 4 ) i.e ( 2 , 3 ) be ( x₁ , y₁ ).

`\large{ \tt{✎ \: LET'S \: START}} :`

`☯ \: \boxed { \large{\tt{y - y_(1) = m(x - x_(1))}}}`

`\large{ \tt{↬y - 3 = 3(x - 2)}}`

`\large{ \tt{↬y - 3 = 3x - 6}}`

`\large{ \tt{↬3x - 6 = y - 3}}`

`\large{ \tt{↬3x - y - 6 + 3 = 0}}`

`\large{ \tt{↬ \boxed{ \tt{3x - y - 3 = 0}}}}`

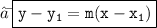
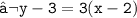
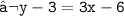
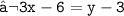
• Hence , The required equation of a straight line is 3x - y - 3 = 0 .

`\tt{✺ \: CHOOSE \: YOUR \: HABITS \: CAREFULLY \: ,THEY \: DECIDE \: YOUR \: FUTURE! \: ♪}`

۵Hope I helped ! ツ

☼Have a wonderful day / evening ! ☃

# StayInAndExplore ! ☂

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁