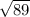Question

Please help me do this question I will really appreciate it

Answer 1

Repeat with

(x₁, y₁ ) = L(- 6, - 6) and (x₂, y₂ ) = L'(- 1, 2)

LL' = \sqrt{(-1+6)^2+(2+6)^2}

(−1+6)

2

+(2+6)

2

= \sqrt{5^2+8^2}

5

2

+8

2

= \sqrt{25+64}

25+64

= \sqrt{89}

89

Explanation:

Repeat with

(x₁, y₁ ) = L(- 6, - 6) and (x₂, y₂ ) = L'(- 1, 2)

LL' = \sqrt{(-1+6)^2+(2+6)^2}

(−1+6)

2

+(2+6)

2

= \sqrt{5^2+8^2}

5

2

+8

2

= \sqrt{25+64}

25+64

= \sqrt{89}

89

Answer 2

all
`√(89)`

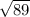
Explanation:

Calculate the lengths using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

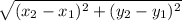
with (x₁, y₁ ) = J(- 2, - 2) and (x₂, y₂ ) = J'(3, 6)

JJ' =
`√((3+2)^2+(6+2)^2)` =
`√(5^2+8^2)` =
`√(25+64)` =
`√(89)`

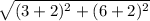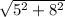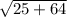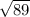
Repeat with

(x₁, y₁ ) = K(- 8, - 4) and (x₂, y₂ ) = K'(- 3, 4)

KK' =
`√((-3+8)^2+(4+4)^2)` =
`√(5^2+8^2)` =
`√(25+64)` =
`√(89)`

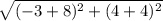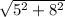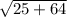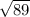
Repeat with

(x₁, y₁ ) = L(- 6, - 6) and (x₂, y₂ ) = L'(- 1, 2)

LL' =
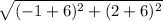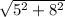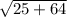`√((-1+6)^2+(2+6)^2)` =
`√(5^2+8^2)` =
`√(25+64)` =
`√(89)`