Given:
Height of the lighthouse = 280 feet
The angle of depression from the top of the lighthouse to a ship = 18°.
To find:
The distance between boat and shore.
Solution:
Draw a diagram by using the given information.
In a right angle triangle,
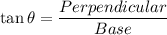
In triangle ABC,
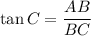
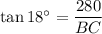
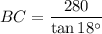
Using a calculator, we get
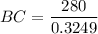
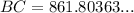
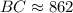
Therefore, the boat is 862 feet away from shore.