Answer:
The predicted number of views on a video that's been posted for 222 days is approximately 3.1459567 × 10⁷⁵ views
Step-by-step explanation:
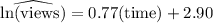
The given parameters for the exponential relationship between the number of views and the duration after posting a video is presented as follows;
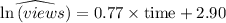
For a video that has been posted 222 days, we have;
Time = 222 days
Therefore, we get;
ln(views) = 0.77 × 222 + 2.90 = 173.84
∴ The predicted number of views on a video that's been posted for 222 days = e^173.84 = 3.1459567 × 10⁷⁵