Question

Identify the value for C in the following equation that would make the conic section a parabola: 2x2 + Cy2 + 3x + 5y + 1 = 0

Answer 1

Given:

The conic equation is:

`2x^2+Cy^2+3x+5y+1=0`

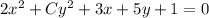
To find:

The value of C such that the given conic equation make a parabola.

Solution:

The general for of conic equation is:

`Ax^2+Cy^2+Dx+Ey+F=0`

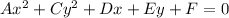
This equation represents a parabola is either A=0 or C=0 but not both equal to zero.

The given equation is:

`2x^2+Cy^2+3x+5y+1=0`

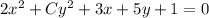
Here, coefficient of
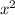`x^2` is A=2 and coefficient of [tec]y^2[/tex] is C.

Since A is not equal to 0, therefore C must be equal to 0 to form a parabola.

Therefore, the only value of C is 0.