Question

Please show how you did it so I can learn​

Answer 1

c) No Real Solution

Explanation:

I'ma try my best to explain it!

We have: 4x^2+5x=−10

Step 1: Subtract -10 from both sides.

4x^2+5x−(−10)=−10−(−10) (you don't put the -10 next to it but you put it in the bottom)

Then we get 4x^2+5x+10=0 from the subtraction above

For this equation: a=4, b=5, c=10

4x^2+5x+10=0

Then we use quadratic formula with a=4, b=5, c=10

The answer is the picture below: means no solution

Hope this helps and is correct!

Answer 2

C

Explanation:

We have the equation:

`4x^2+5x=-10`

Add 10 to both sides to isolate the equation.

`4x^2+5x+10=0`

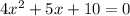
This is not factorable*, so we can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

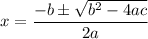
In this case, a = 4, b = 5, and c = 10.

Substitute:

`\displaystyle x=(-(5)\pm√((5)^2-4(4)(10)))/(2(4))`

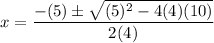
Simplify:

`\displaystyle x=(-5\pm√(-135))/(8)`

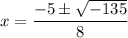
Since we cannot take the root of a negative, we have no real solutions.

Our answer is C.

*To factor something in the form of:

`ax^2+bx+c=0`

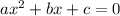
We want two numbers p and q such that pq = ac and p + q = b.

Since ac = 4(10) = 40. We need to find two whole numbers that multiply to 40 and add to 5.

No such numbers exist, so the equation is not factorable.