1 Answer

Ask a Question

Runar Jordahl · Answer 1 · 2023-12-09T09:49:26+0000

First of all find the total area and then subtract the area of circle from the area of rectangle, It will be easier that way...

$\red{ \rule{35pt}{2pt}} \orange{ \rule{35pt}{2pt}} \color{yellow}{ \rule{35pt} {2pt}} \green{ \rule{35pt} {2pt}} \blue{ \rule{35pt} {2pt}} \purple{ \rule{35pt} {2pt}}$

Finding area of rectangle:

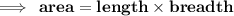
$\qquad \bf \implies \: area = length * breadth$

Length = 3 cm
Breadth = 4 cm

$\qquad \tt \blue\looparrowright \purple{area = 3 * 4}$

$\qquad \tt \blue\looparrowright \purple{area = 12 \: {cm}^(2) }$

Finding area of circle:

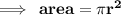
$\qquad \bf \implies \: area = \pi {r}^(2)$

π = 22/7
r = 1

$\qquad \tt \red\looparrowright \green{area = (22)/(7) * {1}^(2) }$

$\qquad \tt \red\looparrowright \green{area = (22)/(7) * 1}$

$\qquad \tt \red\looparrowright \green{area = 3.14 \: {cm}^(2) }$

Find the area of shaded region now,

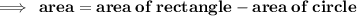
$\qquad \bf \implies \: area =area \: of \: rectangle - area \: of \: circle$

Area of rectangle = 12 cm²
Area of circle = 3.14 cm²

$\qquad \tt \pink\looparrowright \orange{area = 12 - 3.14 }$

$\qquad \tt \pink\looparrowright \orange{area = 8.86}$

➪ Thus, The area of the shaded region is 8.86 cm²...~

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.