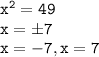Question

PLEAS HELP ILL GIVE YOU 100 POINTSS!! NEED BY SUNDAY

1) Which of the following methods would be the easiest to use to solve x^2−6=0?


All three methods would be easy and effective.


A. factoring


B. using the quadratic formula


C. isolating the x2 term and finding the square root of both sides
2)Which of the following methods would be the easiest to use to solve x^2−11=0?


A. factoring


B. All three methods would be easy and effective.


C. using the quadratic formula


D. isolating the x2 term and finding the square root of both sides
3) Which of the following methods would be the easiest to use to solve x^2−11=0?


A. factoring


B. All three methods would be easy and effective.


C. using the quadratic formula


D. isolating the x2 term and finding the square root of both sides
4)Which equation would be the best to solve by completing the square?


A. 3x^2+4x=−2

B. x^2 + 11x = 40


C. x^2 = 49


D. x^2 + 10x = 75

Answer 1

Which of the following methods would be the easiest to use to solve x²−6=0?

• C. isolating the x² term and finding the square root of both sides.

Solution ⤵️

`\tt \: {x}^(2) - 6 = 0 \\ \tt {x}^(2) = 6 \\ \tt \: x = \pm √(6) \\ \tt \: x = - √(6) , x = √(6)`

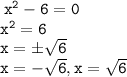
And done, Solved!

`\red{ \rule{35pt}{2pt}} \orange{ \rule{35pt}{2pt}} \color{yellow}{ \rule{35pt} {2pt}} \green{ \rule{35pt} {2pt}} \blue{ \rule{35pt} {2pt}} \purple{ \rule{35pt} {2pt}}`

Which of the following methods would be the easiest to use to solve x²−11=0?

• D. isolating the x² term and finding the square root of both sides

`\tt {x}^(2) - 11 = 0 \\ \tt \: {x}^(2) = 11 \\ \tt \: x = \pm √(11) \\ \tt \: x = - √(11) , x = √(11)`

`\red{ \rule{35pt}{2pt}} \orange{ \rule{35pt}{2pt}} \color{yellow}{ \rule{35pt} {2pt}} \green{ \rule{35pt} {2pt}} \blue{ \rule{35pt} {2pt}} \purple{ \rule{35pt} {2pt}}`

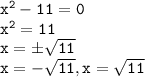
Which equation would be the best to solve by completing the square?

• The equation in option C will be the best because the constant in the equation is a perfect square root...

`\tt {x}^(2) = 49 \\ \tt \: x = \pm7 \\ \tt \: x = - 7, x = 7`