Answer:
Approximately 198 grams will remain in the sample after 12 hours.
Approximately 1.09 grams will remain after three days.
Explanation:
We can write an exponential function to model the situation. The exponential model for decay is:
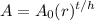
Where A₀ is the initial amount, r is the rate of decay, t is the time that has passed (in this case in hours), and h is the half-life.
Since the half-life of the chemical, astatine, is 8 hours, h = 8 and r = 0.5. The initial amount is 560 grams. Hence:
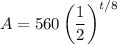
To find when the sample will have approximately 198 grams, remaining, let A = 198 and solve for t:
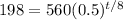
Solve for t:
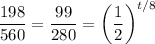
Take the natural log of both sides:

Using logarithm properties:
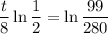
So:
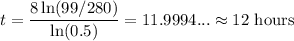
Approximately 198 grams remain in the sample after 12 hours.
Three days is equivalent to 72 hours. Hence, t = 72:
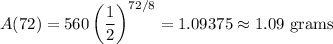
Approximately 1.09 grams of astatine will remain after three days.