Question

Don't just say the answer, please show how you got it so I can know for further use​

Answer 1

C

Explanation:

We have the equation:

`x^2-6x=10`

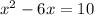
We can subtract 10 from both sides:

`x^2-6x-10=0`

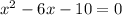
Since this equation isn't factorable, we can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

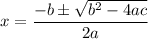
In this case, a = 1, b = -6, and c = -10.

Substitute:

`\displaystyle x=(-(-6)\pm√((-6)^2-4(1)(-10)))/(2(1))`

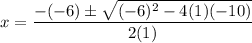
Simplify:

`\displaystyle x=(6\pm√(76))/(2)`

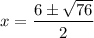
Note that:

`√(76)=√(4\cdot 19)=2√(19)`

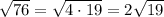
Hence:

`\displaystyle x=(6\pm2√(19))/(2)=3\pm√(19)`

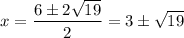
Therefore, our answer is C.