Question

A loaded spring launches a 2.50 kg block, using a force of 450 N. If the change in

momentum is 12.0 kg*m/s, how long was the block in contact with the spring?

Answer 1

37.5 seconds

Step-by-step explanation:

The given parameters are;

The mass of the block on the spring, m = 2.50 kg

The force with which the loaded spring launches the block, F = 450 N

The change in momentum of the block, Δp = 12.0 kg·m/s

We have;

Let the force with which the block was launched = The net force,
`F_(NET)`

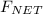
By Newton's second law of motion, we have;

F =
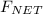`F_(NET)` = Δp × Δt

Where;

Δt = The time the block is in contact with the spring

Therefore;

`\Delta t = (F_(NET))/(\Delta p)`

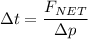
By plugging in the values for
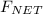`F_(NET)` and Δp, we have;

`\Delta t = (450 \ N)/(12.0 \ kg \cdot m/s) = 37.5 \ s`

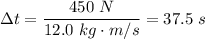
The time duration the block is in contact with the spring, Δt = 37.5 seconds.