1 Answer

Kibaekr · Answer 1 · 2022-07-06T17:45:34+0000

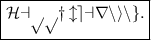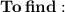
$\huge\bold{To\:find :}$

The value of
.

$\large\mathfrak{{\pmb{\underline{\orange{Solution}}{\orange{:}}}}}$

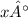The value of
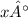is 150°. ✅

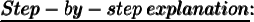
$\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\orange{:}}}}}$

We know that,

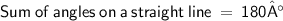
$\sf\purple{Sum\:of\:angles\:on\:a\:straight\:line\:= \:180°}$

➡ 81° +
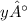= 180°

➡
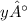= 180° -81°

➡
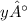= 99°

Since an exterior angle of a triangle is equal to the sum of the two opposite interior angles, we have

=
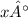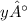+ 51°

Substituting the value of ''
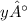" in the above equation,

➪
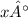= 99° + 51°

➪
= 150°

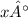$\sf\red{Therefore, \:the\: value \:of \:x°\: is \:150°.}$

Note:-

Kindly refer to the attached file.

${\boxed{\mathcal{\blue{Happy\:learning .}}}}$

Please log in or register to add a comment.